Fenceposts and calendars

One thing I’ve always had trouble reasoning about is problems that involve spans and numbers, or for practical purposes, problems with clocks and calendars. It’s not just that I make what computer scientists call “fenceposts errors”, it’s not so much a matter of “oops” as “huh?!”. I don’t trust my arithmetic. Obviously I can do addition/subtraction, but what I can’t do is trust myself to avoid a fencepost error. So at age 33, I’m still reduced to counting on my fingers and muttering aloud when given a timespan and target to work with. My latest enemy is this:

Any 12 consecutive months in a period 15 months immediately prior to the date of application (21 March).

For me, this sort of thing can be a struggle. Trying to figure out if say the period of 29 Feb can not just take me effort but also leave me in a perpetual state of doubt about whether I’ve made some kind of silly mistake or another. Have I fence-posted? Have I confused the end of the month with the end of the period? Etc. Again, these don’t manifest as a concsiously manipulable checklist of potential errors but sort of a mental fog.

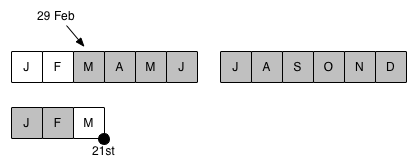
This morning, I may have worked out a visual technique that seems to work with my brain for this exact problem, as in the example below:

1. I represent the spans (months) as boxes, lining up one row of boxes for a year, split into two halves so I’m less likely to miscount.

2. I use as many boxes as the length of the desired span, here 15 boxes for 15 months (but still one row per calendar year, eg first row for 2012)

3. I denote the end date of the period in question on the boundary of a box, so the bottom-right corner corresponds to 21st March (and not 30 March)

4. I can then use the boundaries to reason about other dates. For exmaple, in the below, I know that the 29th of Feb follows the boundary of the Feburary box.

5. And I can then count the boxes like I would count on my fingers.

“Draw a picture” may sound like pretty obvious/uninteresting advice. But it’s really about the details, the decisions around say the meaning of the right boundary (end of the month? or date in question?). I’m not sure how well this generalises to other problems, but it does seem to lend itself to back-of-the-envelope style calculations. The important thing is to have the right sort of redundant visual cues to ensure confidence about the problem at hand, and with this little diagram, I think I’m OK with the 29th of February.